ALGEBRA
Mathematics where letters (example: X, V or U) and other general symbols are used to represent numbers and quantities in equationsThe equal sign =
The symbol shows what is on the left of the symbol is the same as what is on the right.
Example
4 = 1+ 1 + 1 + 1
Using the balance
The diagram (a simple balance) is balanced because it is horizontal (straight line parallel to the table) and we can say that the left side is equal to the right side
Example
Four red balls are placed on the right size of the balance. The balance tilted towards the right because the right size is heavier. Now, the left and right sides are not balanced or equal anymore.
Forming an equation
We have U, X, and Y. Which alphabets make both sides equal?
X is heavier than the 4 red balls
Both sides are balanced. V (the left side) = 4 red balls (right side)
V = 4 red balls. V balances both sides.
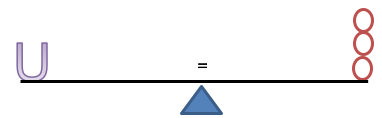
U is lighter than the 4 red balls
We have U, X, and Y. Which alphabets make both sides equal?
What is X?
Since X (the left side) is heavier than the 4 red balls (the right side), we can add more red balls to try to balance both side.
After adding 1 red ball, both sides are still not balanced, we can add another red ball.
After adding 1 red ball, both sides are balanced.
X = 6 red balls
What is U?
Since U (the left side) is lighter than the 4 red balls (the right side), we must by reduce or ‘lighten’ the right side. Remove 1 red ball from the right.
Both sides are balanced or equal.
U = 3 red balls.
Forming An Equation
2U = 6 is an equation
An equation has
(1) Variables (those letters U, V, X)
(2) equal sign =
(3) number (2, 6, 14m, 9 kg)
(4) operators (+ , - , x , ¸)
We solve the equation to find the value of the variable that make the equality true.
This is also an equation:
3X + 2 = 8
An equation can also have
Example
Form an equation from the diagram and find the value of U
In an equation
U + 1 = 4
The variable is on the left side and equal to values(number) on the right side.
Moving the number (+1) to the right side by minus 1.
We need to also minus 1 from the right side
Balancing the equation,
We minus 1 from the LEFT SIDE AND the RIGHT SIDE
U + 1 – 1 = 4 - 1
U = 3
Example
Find the value of X
X + 2 = 6
X + 2 = 6 (Remove number from left side)
X + 2 – 2 = 6 – 2 (by -2 from both side)
X = 6 – 2
= 4
Example
Solve 12 = U + 5
METHOD:
Step 1: WRITE L=R and equation, putting variable to left side
L = R
12 = U + 5
U + 5 = 12
Step 2: Move all numbers to right
A + 5 – 5 = 12 – 5
A = 12 - 5
A = 7
Example
Solve A – 7 = 14
Step 1: L = R
A – 7 = 14
Step 2 : A – 7 + 7 = 14 + 7
Step 3: A = 21
SOLVE for Non-One VARIABLE
Solve 3U - 2 = 7
We need to find the value of U and not 3U. How do we find U?
There are two ways to change to U:
(I) Divide by itself - > / 3 , 3U / 3 = U
(II) Multiply by x 1/number, 3U x 1/3 = U - > multiply by 1/number
Practice: Fill in the blank
(1) 4U / ____ = U [U = 4]
4U x _____ = U [U = ¼]
(2) 2U / ______ = U [U = 2]
2U x ______ = U [U = ½]
Fractional U, multiply by the inverse
Example:
¾ U x ______ = U
Step: Inverse of ¾ = 4/3
¾ U x 4/3 = U
METHOD to solve an Equation
Example
Solve 3U - 2 = 7
Step 1: WRITE L=R and equation, putting variable to left side
L = R
3U – 2 = 7
Step 2: Move all numbers to right
L = R
3U - 2 + 2 = 7 + 2
Step3: 1-UNIT Variable
L = R
3U = 9
3 3 Solve the equation
U = 3
Finding The Value Of An Equation
When the variable is given a value, replace the variables with the value.
Example
Find the value of the equation when A = 4
(1) 4 + A
= 4 + 4 (replace A with A = 4)
= 8
(2) ½ A + 3
= ½ x 4 + 3 (replace A with A = 4)
= 2 + 3
= 5
(3) 5A / 2 + 8
= 5/2 x 4 + 8 (replace A with A = 4)
= 5 x 2 + 8
=10 + 8 = 18
~~~~ END ~~~~ :)
